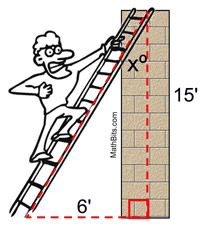
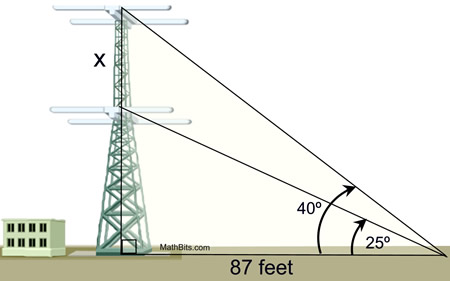
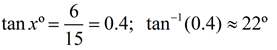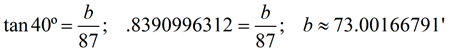Simple equations on Surds
Numbers such as 6, 0.37, 0.6 can be express as exact fractions or ratio: 6/1, 37/100, 2/3. these are called rational numbers.
General Rules for Solving Surd
Split
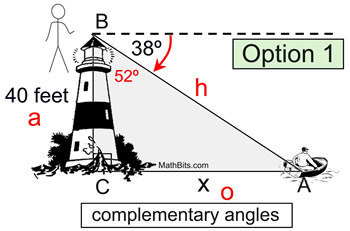
by searching for factors of 50 whereby at least one of them must be a perfect square.
Following this rule, the factors should be either 5 & 10 or 25 & 2 or 50 & 1 but 25 & 2 should be the most appropriate factor here because you can at least find the square root of 25 which makes it a perfect square.
Solution
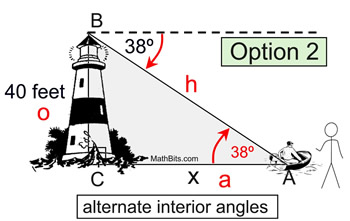
Factors of 32 will be 16 & 2;
Note that at least one of the factors must be a perfect square.
Solution
Numbers such as 6, 0.37, 0.6 can be express as exact fractions or ratio: 6/1, 37/100, 2/3. these are called rational numbers.
Numbers which cannot be written as ratio are called irrational or non-rational numbers. pie is an example of an irrational number.
pie= 3.141592....
Methods
of Manipulating Surd
1. Simplification of Surd
2. Addition & Subtraction of Surd
3. Multiplication & Division of Surd
4. Conjugate of a Surd
General Rules for Solving Surd
1. Figures with figures and roots with roots.
2. When multiplying roots of similar values, you remove the
roots and take only one of the values.
1.
Simplification of Surd
Examples;
Split
by searching for factors of 50 whereby at least one of them must be a perfect square.
Following this rule, the factors should be either 5 & 10 or 25 & 2 or 50 & 1 but 25 & 2 should be the most appropriate factor here because you can at least find the square root of 25 which makes it a perfect square.
Solution
Factors of 32 will be 16 & 2;
Note that at least one of the factors must be a perfect square.
Solution