Solving Equations on Venn Diagrams

 Solving Equations on Venn Diagrams

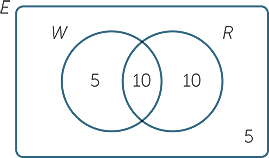
Last June, there were 15 windy days and 20 rainy days, yet 5 days were neither windy nor rainy.’

How can this be, when June only has 30 days? A Venn diagram, and the language of sets, easily sorts this out.

Let W be the set of windy days,
and R be the set of rainy days.
Let E be the set of days in June.
Then W and R; together have size 25, so
the overlap between W and R is 10.; The Venn diagram opposite displays; the whole situation.

The purpose of this module is to introduce language for talking about sets, and some notation for setting out calculations, so that counting problems such as this can be sorted out. The Venn diagram makes the situation easy to visualise.

Content

Describing and naming sets

A set is just a collection of objects, but we need some new words and symbols and diagrams to be able to talk sensibly about sets.

In our ordinary language, we try to make sense of the world we live in by classifying collections of things. English has many words for such collections. For example, we speak of ‘a flock of birds’, ‘a herd of cattle’, ‘a swarm of bees’ and ‘a colony of ants’.

We do a similar thing in mathematics, and classify numbers, geometrical figures and other things into collections that we call sets. The objects in these sets are called the elements of the set.

Describing a set

A set can be described by listing all of its elements. For example,

S = { 1, 3, 5, 7, 9 },

which we read as ‘S is the set whose elements are 1, 3, 5, 7 and 9’. The five elements of the set are separated by commas, and the list is enclosed between curly brackets.

A set can also be described by writing a description of its elements between curly brackets. Thus the set S above can also be written as

S = { odd whole numbers less than 10 },

which we read as ‘S is the set of odd whole numbers less than 10’.

A set must be well defined. This means that our description of the elements of a set is clear and unambiguous. For example, { tall people } is not a set, because people tend to disagree about what ‘tall’ means. An example of a well-defined set is

T = { letters in the English alphabet }.

Equal sets

Two sets are called equal if they have exactly the same elements. Thus following the usual convention that ‘y’ is not a vowel,

{ vowels in the English alphabet } = { a, e, i, o, u }

On the other hand, the sets { 1, 3, 5 } and { 1, 2, 3 } are not equal, because they have different elements. This is written as

{ 1, 3, 5 } ≠ { 1, 2, 3 }.

The order in which the elements are written between the curly brackets does not matter at all. For example,

{ 1, 3, 5, 7, 9 } = { 3, 9, 7, 5, 1 } = { 5, 9, 1, 3, 7 }.

If an element is listed more than once, it is only counted once. For example,

{ a, a, b } = { a, b }.

The set { a, a, b } has only the two elements a and b. The second mention of a is an unnecessary repetition and can be ignored. It is normally considered poor notation to list an element more than once.

The symbols ∈ and ∉

The phrases ‘is an element of’ and ‘is not an element of’ occur so often in discussing sets that the special symbols ∈ and ∉ are used for them. For example, if A = { 3, 4, 5, 6 }, then

3 ∈ A (Read this as ‘3 is an element of the set A’.)

8 ∉ A (Read this as ‘8 is not an element of the set A’.)

Describing and naming sets

• A set is a collection of objects, called the elements of the set.
• A set must be well defined, meaning that its elements can be described and
  listed without ambiguity. For example:

{ 1, 3, 5 } and { letters of the English alphabet }.

• Two sets are called equal if they have exactly the same elements.
• The order is irrelevant.
• Any repetition of an element is ignored.
• If a is an element of a set S, we write a ∈ S.
• If b is not an element of a set S, we write b ∉ S.

EXERCISE 1

a

Specify the set A by listing its elements, where
A = { whole numbers less than 100 divisible by 16 }.

b

Specify the set B by giving a written description of its elements, where
B = { 0, 1, 4, 9, 16, 25 }.

c

Does the following sentence specify a set?
C = { whole numbers close to 50 }.

Finite and infinite sets

All the sets we have seen so far have been finite sets, meaning that we can list all their elements. Here are two more examples:

{ whole numbers between 2000 and 2005 } = { 2001, 2002, 2003, 2004 }

{ whole numbers between 2000 and 3000 } = { 2001, 2002, 2003,…, 2999 }

The three dots ‘…’ in the second example stand for the other 995 numbers in the set. We could have listed them all, but to save space we have used dots instead. This notation can only be used if it is completely clear what it means, as in this situation.

A set can also be infinite − all that matters is that it is well defined. Here are two examples of infinite sets:

{ even whole numbers } = { 0, 2, 4, 6, 8, 10, …}

{ whole numbers greater than 2000 } = { 2001, 2002, 2003, 2004, …}

Both these sets are infinite because no matter how many elements we list, there are always more elements in the set that are not on our list. This time the dots ‘…’ have a slightly different meaning, because they stand for infinitely many elements that we could not possibly list, no matter how long we tried.

The numbers of elements of a set

If S is a finite set, the symbol | S | stands for the number of elements of S. For example:

If S = { 1, 3, 5, 7, 9 }, then | S | = 5.

If A = { 1001, 1002, 1003, …, 3000 }, then | A | = 2000.

If T = { letters in the English alphabet }, then | T | = 26.

The set S = { 5 } is a one-element set because | S | = 1. It is important to distinguish between the number 5 and the set S = { 5 }:

5 ∈ S but 5 ≠ S .

The empty set

The symbol ∅ represents the empty set, which is the set that has no elements at all. Nothing in the whole universe is an element of ∅:

| ∅ | = 0 and x ∉ ∅, no matter what x may be.

There is only one empty set, because any two empty sets have exactly the same elements, so they must be equal to one another.

Finite and Infinite sets

• A set is called finite if we can list all of its elements.
• An infinite set has the property that no matter how many elements we list,
  there are always more elements in the set that are not on our list.
• If S is a finite set, the symbol | S | stands for the number of elements of S.
• The set with no elements is called the empty set, and is written as ∅.
  Thus | ∅ | = 0.
• A one-element set is a set such as S = { 5 } with | S | = 1.

EXERCISE 2

a

Use dots to help list each set, and state whether it is finite or infinite.

i

B = { even numbers between 10 000 and 20 000 }

ii

A = { whole numbers that are multiples of 3 }

b

If the set S in each part is finite, write down | S |.

i

S = { primes }

ii

S = { even primes }

iii

S = { even primes greater than 5 }

iv

S = { whole numbers less than 100 }

c

Let F be the set of fractions in simplest form between 0 and 1 that can be written with a single-digit denominator. Find F and | F |.

Subsets and Venn diagrams

Subsets of a set

Sets of things are often further subdivided. For example, owls are a particular type of bird, so every owl is also a bird. We express this in the language of sets by saying that the set of owls is a subset of the set of birds.

A set S is called a subset of another set T if every element of S is an element of T. This is written as

S ⊆ T (Read this as ‘S is a subset of T’.)

The new symbol ⊆ means ‘is a subset of’. Thus { owls } ⊆ { birds } because every owl is a bird. Similarly,

if A = { 2, 4, 6 } and B = { 0, 1, 2, 3, 4, 5, 6 }, then A ⊆ B,

because every element of A is an element of B.

The sentence ‘S is not a subset of T’ is written as

S T.

This means that at least one element of S is not an element of T. For example,

{ birds } 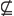{ flying creatures }

because an ostrich is a bird, but it does not fly. Similarly,

if A = { 0, 1, 2, 3, 4 } and B = { 2, 3, 4, 5, 6 }, then A B,

because 0 ∈ A, but 0 ∉ B.

The set itself and the empty set are always subsets

Any set S is a subset of itself, because every element of S is an element of S. For example:

{ birds } ⊆ { birds } and { 1, 2, 3, 4, 5, 6 } = { 1, 2, 3, 4, 5, 6 }.

Furthermore, the empty set ∅ is a subset of every set S, because every element of the empty set is an element of S, there being no elements in ∅ at all. For example:

∅ ⊆ { birds } and ∅ ⊆ { 1, 2, 3, 4, 5, 6 }.

Every element of the empty set is a bird, and every element of the empty set is one of the numbers 1, 2, 3, 4, 5 or 6.

Subsets and the words ‘all’ and ‘if … then’

A statement about subsets can be rewritten as a sentence using the word ‘all’.
For example,

{ owls } ⊆ { birds }		means		‘All owls are birds.’
{ multiples of 4 } ⊆ { even numbers }		means		‘All multiples of 4 are even.’
{ rectangles } ⊆ { rhombuses }		means		‘Not all rectangles are rhombuses.’

They can also be rewritten using the words ‘if … then’. For example,

{ owls } ⊆ { birds }		means		‘If a creature is an owl, then it is a bird.’
{ multiples of 4 } ⊆ { even numbers }		means		‘If a number is a multiple of 4, then it is even’:
{ rectangles } ⊆ { rhombuses }		means		‘If a figure is a rectangle, then it may not be a square.’

Venn diagrams

Diagrams make mathematics easier because they help us to see the whole situation at a glance. The English mathematician John Venn (1834−1923) began using diagrams to represent sets. His diagrams are now called Venn diagrams.

In most problems involving sets, it is convenient to choose a larger set that contains all of the elements in all of the sets being considered. This larger set is called the universal set, and is usually given the symbol E. In a Venn diagram, the universal set is generally drawn as a large rectangle, and then other sets are represented by circles within this rectangle.

For example, if V = { vowels }, we could choose the universal set as E = { letters of the alphabet } and all the letters of the alphabet would then need to be placed somewhere within the rectangle, as shown below.

In the Venn diagram below, the universal set is E = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }, and each of these numbers has been placed somewhere within the rectangle.

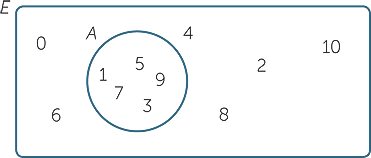
The region inside the circle represents the set A of odd whole numbers between 0 and 10. Thus we place the numbers 1, 3, 5, 7 and 9 inside the circle, because A = { 1, 3, 5, 7, 9 }. Outside the circle we place the other numbers 0, 2, 4, 6, 8 and 10 that are in E but not in A.